The Math Behind the Jury Selection Problem

I recently served on the jury for a trial in the county superior court system, and contrary to popular belief it turned out to be an interesting experience. The ordeal gave me confidence in the idea of being judged by a jury of one’s peers, and I came away with an appreciation of the fact that the responsibilities of a jury are precise and straightforward, much like the role of computer hardware (jurors) carrying out the instructions of a software program (law) given a set of well-defined inputs (evidence).

As I sat through the initial jury selection process, I also got to thinking about some of the mathematics behind the process. In particular, is there a way to answer the two questions on every prospective juror’s mind: will I be selected as a juror and how long is this process going to take?

The jury selection process used in the American court system can be formulated as an online variant of the secretary problem, where the task is to hire the k best secretaries (jurors) from a pool of n candidates (jury pool). During jury selection, the prospective jurors are interviewed one by one and an immediate decision is made to select the candidate as part of the jury, or to excuse the candidate from service. It is assumed that there exists a way to rank the entire pool of candidates from best to worst, and that this method is employed by the judge and attorneys during the selection process to evaluate jurors on a relative basis.

It turns out that the problem is a generalized version of the secretary problem, and there exists an optimal strategy for performing such a selection process as to maximize the probability of selecting the top k jurors from the jury pool¹. The idea is to choose a cutoff value r, and to interview and immediately excuse the first r prospective jurors while remembering the best amongst the first r candidates interviewed. Starting with the r+1 candidate, every candidate that is better than the best candidate interviewed in the initial r prospective jurors is selected, until k jurors have been selected or the pool is exhausted.

To maximize the probability of selecting the top k jurors from a pool of n candidates, the optimal value for r turns out to be

$$\left\lfloor\frac{n}{ke^\frac{1}{k}}\right\rfloor$$

For example, to select twelve jurors and three alternates (k = 15) from a pool of eighty prospective jurors (n = 80), the optimal cutoff is r = 4. That is, the judge and attorneys should interview and excuse the first four candidates, then begin selecting every subsequent candidate that proves better suited for the case than the best candidate amongst the first four interviewed.

With the optimal strategy in hand, we can also compute the expected number of prospective jurors that will be interviewed and evaluated before the final k are selected when such a strategy is employed. By way of simulation, to select 15 jurors from a pool of 80 prospective jurors, the expected number of candidates that will be interviewed during the process is approximately 66, which turns out to be quite close to the number of candidates actually interviewed during my recent experience with the jury selection process with n = 80. For k = 15, here are some more values for the expected number of prospective jurors that will be interviewed, for several different pool sizes:

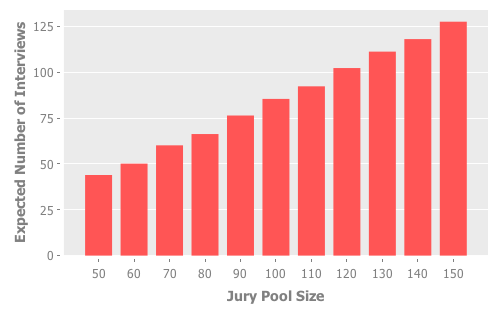
Of course, the actual jury selection process may slightly differ by jurisdiction, and if so the optimal strategy will also differ. For example, the selection process I went through is more akin to a mini-batch online version of the problem, where a small batch of candidates are interviewed together before the judge and attorneys have to decide whether to excuse any of the candidates in the batch. Additionally, there’s a small buffer of candidates that can be kept around during the selection process, and may be excused at later stages.