Doublets (Word Ladder) - A Word Puzzle Game

Doublets (also known as word ladder) is a word puzzle game invented by Lewis Carroll where the objective is to turn one dictionary word into another by changing one letter at a time. At each step, one letter may be changed, and the resulting word must be a valid dictionary word. Much like climbing a ladder where each rung is a word, the goal is reach the target word in as few steps as possible.

For example, to turn “milk” into “wine”, “milk” changes into “mink”, “mink” changes into “mine”, and “mine” changes into “wine”. Each intermediate word is a valid dictionary word. If we are given two arbitrary words, how do we determine the minimal number of intermediate steps needed to transform one word into the other?

Since each transformation is a transition between two valid dictionary words, we need to first figure out a way to generate all the possible words that a given word can turn into by changing only one letter at a time. We can simply go through each character in the word and replace it with each of the 26 character; each changed word should be checked against the dictionary to ensure that it is a valid word.

# Assume we're given a hash of words as the dictionary
def edits(word, dictionary)
  edits = {}
  for i in 0..word.length-1
    # Assuming the word is lowercase, go through each character
    # in the alphabet
    'a'.upto('z') do |c|
      changed = word[0, i] + c + word[i + 1, word.length - 1]
      edits[changed] = true if dictionary[changed]
    end
  end
  return edits.keys
end

The transitions between words can be represented in the form of a graph, where each vertex represents a word and each edge represents a valid transition from one dictionary word to another by changing one letter. Thus, the problem of solving a doublets puzzle boils down to finding the shortest path between the two given words. Since all the edges represent one letter transitions, they are effectively unweighted. Using breadth-first search to search for the word we want to transition to, we are guaranteed to find a solution with the least number of transitions, although there may be alternate solutions with the same number of transitions. Since breadth-first search examines vertices in order of depth - which also happens to be distance from the starting vertex - the algorithm will never prematurely find the end vertex before traversing a path to the vertex that is shorter.

We can see a portion of the graph of transitions for our example of turning “milk” into “wine”.

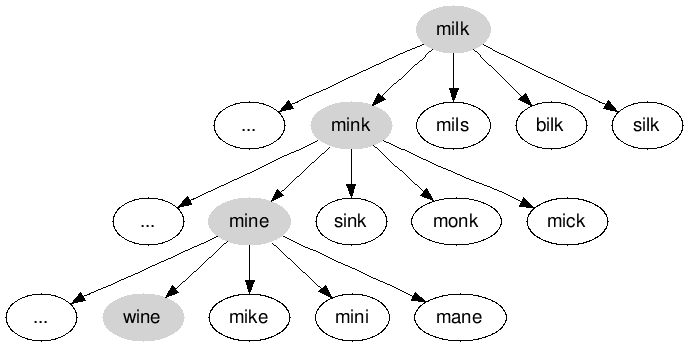
During the traversal, visited vertices will be marked so that they are not examined again. A vertex u will be set as the predecessor of its neighboring vertices v so that we can retrace the word transitions once the traversal terminates. Since the neighbors of each vertex is the set of valid words it can transform into with one-letter changes, we can call the function we defined earlier for each vertex we encounter.

def bfs(start, finish, dictionary)
  visited = {start => true}

  # Keep track of predecessors in the traversal
  pred = {}

  # FIFO queue for vertices
  queue = [start]
  while !queue.empty?
    u = queue.shift

    # Terminate once we've found the finish word
    break if u == finish

    # Visit all the neighboring words of u
    edits(u, dictionary).each do |v|
      unless visited[v]
        pred[v] = u
        queue.push(v)
        visited[v] = true
      end
    end
  end
  return pred
end

By dynamically generating a vertex’s neighbors, the algorithm doesn’t need to go through each word in the dictionary in advance and precompute the graph by generating all of the possible transitions. In the worst case, breadth-first search will examine every vertex and every edge as it traverses the graph. Generating the neighboring transitions for a word requires going through each character in the word, and going through the entire alphabet for each of the characters. Since the alphabet size is constant, the time complexity is linear, or O(n) where n is the length of the word. Since our algorithm will generate transitions for every vertex encountered, the time complexity is O(n|V| + |E|).

When all is said and done, we can put together a program to solve any doublets puzzle. Let’s assume that we have access to a text file of dictionary words, and the text file will be passed in as the an argument to the program.

#!/usr/bin/ruby
file = File.new(ARGV[0], 'r')

# Convert all dictionary words into lowercase, and store them in a hash
dictionary = {}
while line = file.gets
  dictionary[line.strip.downcase] = true
end

start = 'milk'
finish = 'wine'
pred = bfs(start, finish, dictionary)

# Output the words by retracing the path
while !pred[finish].nil?
  puts finish
  finish = pred[finish]
end
puts start